Aufgabe C 1.1
Ein Unternehmer stellt Kunststoffteile her. Erfahrungsgemäß sind 4 % der hergestellten
Teile fehlerhaft.
Die Anzahl fehlerhafter Teile unter zufällig ausgewählten kann als
binomialverteilt angenommen werden.
a) 800 Kunststoffteile werden zufällig ausgewählt.
Berechnen Sie für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:
A: „Genau 30 der Teile sind fehlerhaft.”
B: „Mindestens 5 % der Teile sind fehlerhaft.”
(1,5 VP)
b) Ermitteln Sie, wie viele Kunststoffteile mindestens zufällig ausgewählt werden müssen, damit davon mit einer Wahrscheinlichkeit von mindestens 95 % mindestens 100 Teile keinen Fehler haben.(2 VP)
c) Die Kunststoffteile werden aus Kunststoffgranulat hergestellt. Nach einem Wechsel des Granulats vermutet der Produktionsleiter, dass sich der Anteil der fehlerhaften Teile reduziert hat. Um einen Anhaltspunkt dafür zu gewinnen, ob die Vermutung gerechtfertigt ist, soll die Nullhypothese „Der Anteil der fehlerhaften Teile beträgt mindestens 4 %.” auf der Grundlage einer Stichprobe von 500 Teilen auf einem Signifikanzniveau von 5 % getestet werden.Bestimmen Sie die zugehörige Entscheidungsregel.
(2,5 VP)
Aufgabe C 1.2
Für ein Spiel wird ein Glücksrad verwendet, das drei Sektoren in den Farben rot, grün und blau hat. Für einen Einsatz von 5 Euro darf ein Spieler das Glücksrad dreimal drehen. Erzielt der Spieler dreimal die gleiche Farbe, werden ihm 10 Euro ausgezahlt. Erzielt er drei verschiedene Farben, wird ein anderer Betrag ausgezahlt. In allen anderen Fällen erfolgt keine Auszahlung.
Die Wahrscheinlichkeit dafür, dass dreimal die gleiche Farbe erzielt wird, ist 1/6.
Die Wahrscheinlichkeit dafür, dass dreimal verschiedene Farben erzielt werden, beträgt ebenfalls 1/6.
a) Bei dem Spiel ist zu erwarten, dass sich die Einsätze der Spieler und die Auszahlungen auf lange Sicht ausgleichen.
Berechnen Sie den Betrag, der ausgezahlt wird, wenn drei verschiedene Farben erscheinen.
(1,5 VP)
b) Die ursprünglichen Größen der Sektoren werden geändert. Dabei soll der Mittelpunktswinkel des blauen Sektors größer als 180° werden.Die Abbildung zeigt einen Teil des Baumdiagramms, das für das geänderte Glücksrad die drei Drehungen beschreibt.
Ergänzend ist für einen Pfad die zugehörige Wahrscheinlichkeit angegeben.
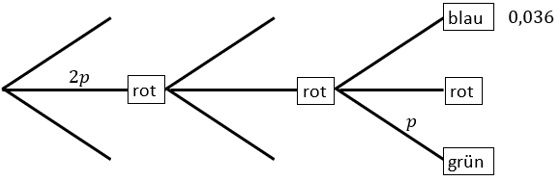
(2,5 VP)
| Downloads |
PowerPoint